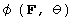 as a function of the temperature
as a function of the temperature 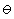 :
:
A schematic of the energy functional 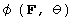 as a function of the temperature
as a function of the temperature 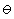 :
:
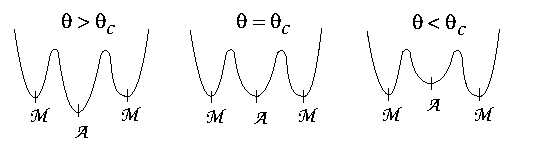
Figure 1: Schematic of the energy functional.
The critical temperature 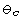 at which both of the phases can coexist in a specimen can be taken as
(As+Ms)/2. This type of energy
functional permits a change of
stability to take place between the phases as the temperature is
changed or stress is applied.
at which both of the phases can coexist in a specimen can be taken as
(As+Ms)/2. This type of energy
functional permits a change of
stability to take place between the phases as the temperature is
changed or stress is applied.
Further, there are multiple energy wells associated with the energy functional depicted in Figure 1: these wells are
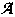 , and
, and
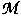 .
.
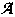 is SO(3) - the set of all rotations; while,
is SO(3) - the set of all rotations; while,
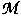 are the union of the sets
are the union of the sets
{RUi for R in SO(3)}for each variant Ui of the martensite phase.
The absolute minimizers of the energy are
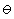 >
>
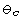 , the minimizers have deformation
gradient F in
, the minimizers have deformation
gradient F in 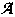 ,
,
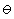 =
=
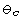 , the minimizers have deformation
gradient F in either
, the minimizers have deformation
gradient F in either 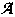 or
or 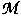 , and
, and
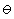 <
<
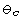 , the minimizers have deformation
gradient F in
, the minimizers have deformation
gradient F in 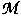 ,
,
Thus, the construction of microstructures reduces to studying deformations which have gradients exclusively from the energy wells. This is called the constrained theory as elastic strains are ignored. If two phases coexist in a specimen or two different martensite variants coexist, then a compatibility equation must be satisfies along the phase boundary.
Top of this page.
Back to the main page.