 in 3-dimensional real space which undergoes the piecewise
constant deformation y as depicted in Figure 1.
in 3-dimensional real space which undergoes the piecewise
constant deformation y as depicted in Figure 1.
As a body transforms, it undergoes a continuous homogeneous deformation, where different regions can have gradient on different energy wells. Thus, a certain compatibility equation must be satisfied.
Consider a specimen occupying some domain  in 3-dimensional real space which undergoes the piecewise
constant deformation y as depicted in Figure 1.
in 3-dimensional real space which undergoes the piecewise
constant deformation y as depicted in Figure 1.
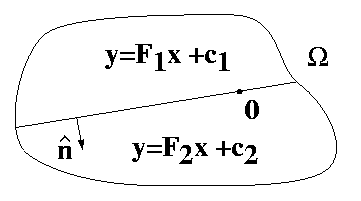
Figure 1: Piecewise constant deformation
In Figure 1, the vectors c are constants, the deformation gradients F are constants and not equal, and the vector n is parallel to the normal of surface of separation.
The deformation depicted in Figure 1 is continuous if and only if;
the vectors c are equal, the vector n is constant, the
surface is a plane, and the the deformation gradients F
satisfy
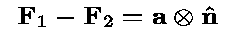
which is called the compatibility equation, and it
is the most equation that needs to be solved in order to
construct microstructures.
If the gradients F1 and F2 are known up to a rotation R in SO(3), then either 0, 1 or 2 solutions may exists to the compatibility equation. A proposition of Ball and James [1], [2] can be used to find if solutions exist and what the exact solutions are.
So, microstructures are various arrangements of the gradients
from different wells, and I have considered several different
combinations which are depicted schematically in Figure 2 below.
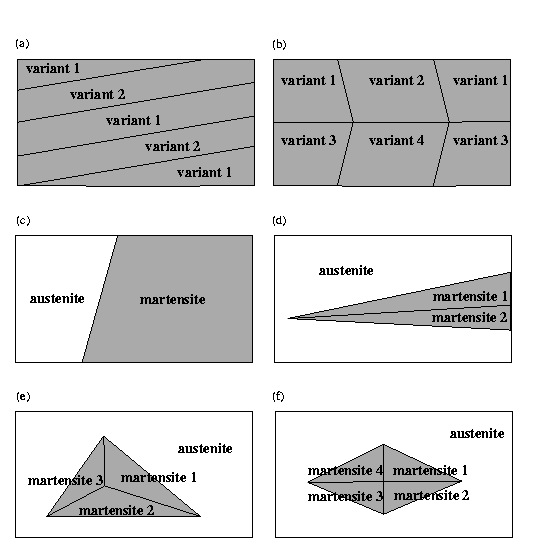
Figure 2: Schematic of microstructures, where (a) twinned martensite, (b) parallelogram, (c), austenite-martensite, (d) wedge, (e) triangle, and (f) diamond.
Go back to the main page and there you will find links to other pages about each of the different microstructures depicted in Figure 2.
Some references are
``Fine phase mixtures as minimizers of energy.'' by John M. Ball and Richard D. James. Archive for Rational Mechanics and Analysis 100, 13 (1987).
``Proposed experimental tests of a theory of fine microstructure and the two-well problem.'' by John M. Ball and Richard D. James. Philosophical Transactions of the Royal Society of London A 338, 389 (1992).
Top of this page.
Back to the main page.