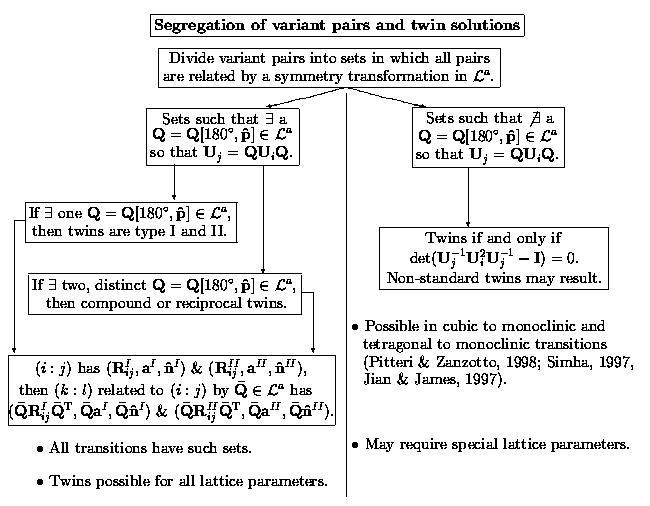
Because all of the variants of the martensite are related by symmetry, then this symmetry can be exploited in the categorization and enumeration of the various realizations of a particular microstructure.
For the twins, the following segregation of variant pairs and solutions of the twinning equation is possible:

The references referred to above are
``Generic and non-generic cubic-to-monoclinic transitions and their twins.'' by Mario Pitteri and Giovanni Zanzotto, Acta Materialia 46, 225 (1997).
``Twin and habit plane microstructure due to the tetragonal to monoclinic transformation of zirconia.'' by Narendra K. Simha. Journal of the Mechanics and Physics of Solids 45, 261 (1997).
``Prediction of microstructure in monoclinic LaNBO4 by energy minimization'' by Li Jian and Richard D. James. Acta Materialia 45, 4271 (1997).
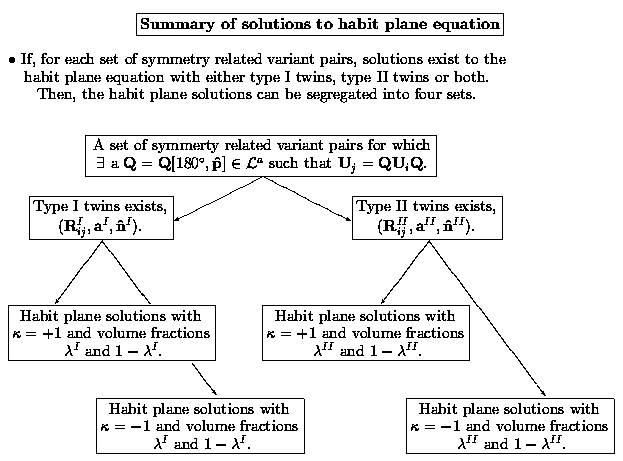
For the solutions to the habit plane equations, the solutions to this equation with different variant pairs and the same twin type have the following symmetry:
The symmetry amongst the habit plane equations can be used to find restrictions on the shape strain and habit plane normal vectors in order for the wedge microstructure to be possible:
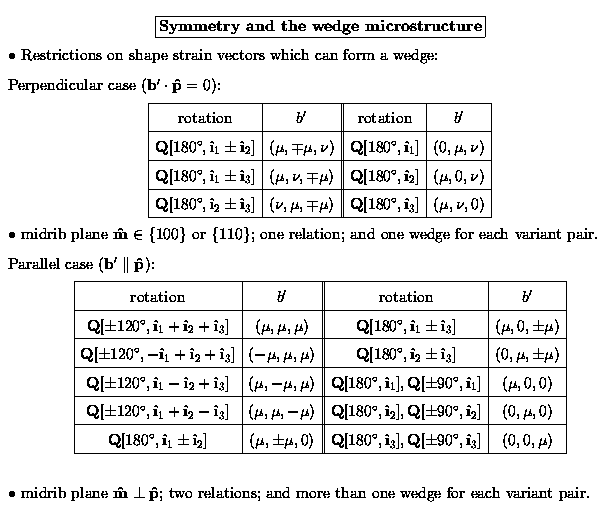
The results about symmetry amongst the twin and habit plane solutions and the exploitation of this symmetry in constructing the wedge is given in
``Symmetry and microstructure in martensites.'' by Kevin F. Hane and Thomas W. Shield. Philosophical Magazine A, 78, 1512 (1998).
Top of this page.
Back to the main page.