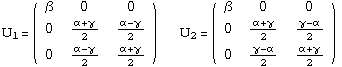
The cubic to orthorhombic transition is described by three parameters: three stretches along three mutually perpendicular directions.
Some alloys undergoing this transition are
There are several possible transitions between a cubic Bravais lattice and an orthorhombic Bravais lattice:
The homogeneous deformation that takes a cubic lattice into an
orthorhombic lattice has gradient denoted as U which is
called a transformation stretch matrix, and for the
cubic-to-orthorhombic transition, there are two kinds of such
matrices [1]. The two kinds of transformation
stretch matrices have
dilatation components exclusively (a diagonal matrix) called orthorhombic ``cubic axes'' variants or
both dilatation and shear components called orthorhombic ` `mixed axes'' variants.
The transformation stretch matrices are the gradient of the deformations which take a cubic lattice into an orthorhombic lattice. There are 6 such matrices, one for each variant of the martensite phase. For the ``mixed axes'' variants, the components are
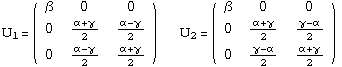
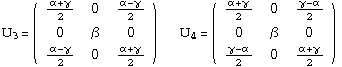
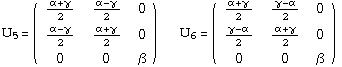
The transformation stretches 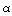 ,
, 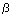 and
and
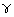 are proportional to
are proportional to
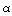 ~
a/ao,
~
a/ao,
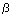 ~
b/ao, and
~
b/ao, and
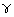 ~
c/ao, respectively, where a, b, and
c are the lattice parameters of the orthorhombic lattice
and ao is the lattice parameter of the cubic lattice.
~
c/ao, respectively, where a, b, and
c are the lattice parameters of the orthorhombic lattice
and ao is the lattice parameter of the cubic lattice.
Here are links to various pages, where a number of different microstructures are discussed. Also contained therein is a table showing the possible microstructures for a cubic-to-orthorhombic transition.
Some references are
`Proposed experimental tests of a theory of fine microstructure and the two-well problem.'' by John M. Ball and Richard D. James. Philosophical Transactions of the Royal Society of London A 338, 389 (1992).
``Wedge-like microstructure in martensites.'' by Kaushik Bhattacharya. Acta Metallurgica et Materialia 39, 2431 (1991).
``Microstructure in a cubic to orthorhombic transition.'' by Kevin F. Hane and Thomas W. Shield. In preparation, 1998.
Top of this page.
Back to the main page.