The transformations under consideration are all symmetry lowering; that is, the lattice of the austenite has higher symmetry than the lattice of the martensite. Consequently, there are multiple configurations of the martensite lattice, and these are called variants.
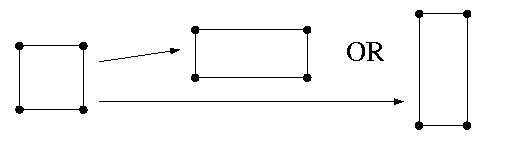
For example, the cubic to tetragonal transition in 2-dimensions has two variants as depicted in Figure 1 below.

Figure 1: Left is a 2-dimensional cubic lattice, and at the right are the two variants of a 2-dimensional tetragonal lattice.
To find all of the variants:
Assume that a transformation stretch matrix U is known;
let Pm denote the point group of the martensite lattice and Pa the point group of the austenite lattice, then there exist an R in Pa such that RURT does not equal U;
form the set S={RURT): R in Pa};
the set of unique elements in S, {Ui} with i = 1 to n, is the variants of martensite; and
the number of variants n is given by the number of elements in Pa divided by the number of elements in Pm.
Possible symmetry lowering transformations between Bravais lattices are given in the table below, where the hexagonal and triclinic lattices are not included.
Symmetry Lowering Transitions |
||
|---|---|---|
| Parent | Product | Number of Variants, n |
| cubic | tetragonal | 3 |
| cubic | trigonal | 4 |
| cubic | orthorhombic | 6 |
| cubic | monoclinic | 12 |
| tetragonal | orthorhombic | 2 |
| tetragonal | monoclinic | 4 |
| orthorhombic | monoclinic | 2 |
| trigonal | monoclinic | 3 |
In the table above, the first column is the crystal structure of the parent phase; the second lists the crystal structure of the product phase; and the last column gives the number of variants of the product phase.
Once all of the variants are known, then the energy functional and its energy wells can be constructed for the material.
Some references are
``Proposed experimental tests of a theory of fine microstructure and the two-well problem.'' by John M. Ball and Richard D. James. Philosophical Transactions of the Royal Society of London A 338, 389 (1992).
`Symmetry and microstructure in martensites.'' by Kevin F. Hane and Thomas W. Shield. Philosophical Magazine A, 78, 1512 (1998).
Top of this page.
Back to the main page.