Other special microstructures are possible besides the wedge and these involve fitting multiple wedge microstructures together. Two such microstructures are the triangle and diamond microstructures, and they are of interest because both can grow from a point on a free surface of the specimen and can exist completely surrounded by the austenite phase. The triangle and diamond microstructures are very special microstructure in that it is only possible in materials with special lattice parameters. Not only must the material be able to form wedges, but the wedges must be able to be fitted together in a compatible manner.
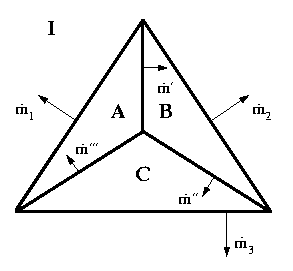
Triangle: The triangle microstructure is a triangular pyramid such that the three habit planes separating the martensite regions from the austenite intersect at a point and through this point passes the line of intersection of the three midrib planes between neighboring martensite regions. The triangles considered have all martensite regions with either single variants of martensite or twinned martensite. Further, the trace of the habit and midrib planes for a triangle on a surface of a specimen are depicted in Figure 1 below:

Figure 1: Triangle microstructure, where the straight lines are the intersection of the habit planes and midrib plane with the plane of the page.
From Figure 1, it can be appreciated that a triangle is possible when a material can form wedges, and any deformation with gradient say A, as in Figure 1, can form a wedge with at least two other deformations with gradients B and C as in Figure 1. In addition, the three habit planes must be non-coplanar, while the three midrib planes must be coplanar. Only materials with very special lattice parameters can form the triangle, and the table below gives the restrictions for several transformations.
Diamond: The diamond microstructure is a diamond pyramid such that the four habit planes separating the martensite regions from the austenite intersect at a point and through this point passes the line of intersection of the four midrib planes between neighboring martensite regions. The diamonds considered have all martensite regions with either single variants of martensite or twinned martensite. The trace of the habit and midrib planes for a diamond on a surface of a specimen are depicted in Figure 2 below:
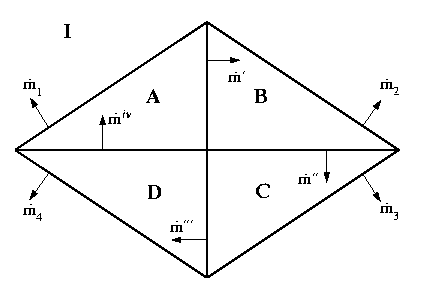
Figure 2: Diamond microstructure, where the straight lines are the intersection of the habit planes and midrib plane with the plane of the page.
Notice that the diamond can be formed by placing two wedges back-to-back, and the diamond is less restrictive than the triangle, because only two non-parallel midrib planes are needed to construct the diamond, but three non-parallel midrib planes are needed for the triangle. Furthermore, the same discussion as for the triangle above applies for the diamond, and the table below gives the restrictions for several transformations.
Various triangle microstructures are possible for different transitions as listed in the table below.
Triangle Microstructures |
||
|---|---|---|
| Transition | Number | Observed |
| Cubic-to-Trigonal | 0 | not possible |
| Cubic-to-Tetragonal | 4 with 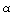 = square
root of 5/3 and = square
root of 5/3 and  =
square root of 1/3 =
square root of 1/3 |
not observed |
| Cubic-to-Orthorhombic | 4 with 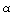 =1
and =1
and 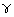 =
f( =
f( )
(*) )
(*) |
not observed |
| " | 12 with  =1
and =1
and 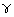 =
g( =
g(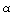 )
(*) )
(*) |
not observed |
| " | 0 with twins | not possible |
| Cubic-to-Monoclinic | 0 | not possible in a particular Ti-Ni alloy (**) |
In the table above, the first column is the transition; the second column lists the number of unique microstructures which can be formed; none of these microstructures have been observed in experiments.
(*) Note: for the cubic to orthorhombic transition, the triangle microstructures is possible if and only if one of the transformation stretches describing the transition is equal to one, and the remaining two satisfy some algebraic condition denoted by the functions f and g. These are the same functions as for the single variant wedge.
(**) Note: for the cubic to monoclinic transition, the triangle is not possible for a particular Ti-Ni alloy, but restrictions as found for the orthorhombic transition may be found.
Various diamond microstructures are possible for different transitions as listed in the table below.
Diamond Microstructures |
||
|---|---|---|
| Transition | Number | Observed |
| Cubic-to-Trigonal | 0 | Not possible |
| Cubic-to-Tetragonal | 0 | Not possible |
| Cubic-to-Orthorhombic | 3 with  =1
and =1
and 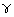 =
g( =
g(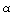 )
(***) )
(***) |
not observed |
| " | 18 on a curve with type I twins | not observed |
| " | 18 on a curve with type II twins | not observed |
| Cubic-to-Monoclinic | 0 | not possible in a particular Ti-Ni alloy (****) |
In the table above, the first column is the transition; the second column lists the number of unique microstructures which can be formed; none of these microstructures have been observed in experiments.
(***) Note: for the cubic to orthorhombic transition, the diamond microstructures is possible if and only if one of the transformation stretches describing the transition is equal to one, and the remaining two satisfy some algebraic condition denoted by the function g. This is the same function as for the single variant wedge. Also, diamonds are possible with twins.
(****) Note: for the cubic to monoclinic transition, there should be a number of surfaces defined by two parameters on which the diamond with twins is possible.
Top of this page.
Back to main page.