Consider a specimen of undistorted austenite occupying some
domain 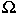 in 3-dimensional
real space.
in 3-dimensional
real space.
The transformation to martensite is through a homogeneous
deformation y = Fx with x in
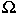
-
This deformation is mapping from a Bravais lattice of the parent phase to a Bravais lattice of the product phase. The deformation gradient F is found from experimental observations of the lattice parameters of the two phases and the change in symmetry.
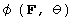 with deformation gradient F in
with deformation gradient F in
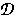 ,
where
,
where 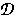 is some subset of the set of
second order tensors, L(3,3), with positive determinant and
temperature
is some subset of the set of
second order tensors, L(3,3), with positive determinant and
temperature 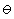 in
I, a subset of the positive real line.
in
I, a subset of the positive real line.
The free energy 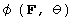 must satisfy certain invariance requirements:
must satisfy certain invariance requirements:
-
frame indifference:
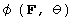 =
= 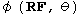 for all R in SO(3) -
the set of proper rotations, and
for all R in SO(3) -
the set of proper rotations, and -
material symmetry:
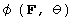 =
= 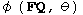 for all Q in
Pa
- the point group of the austenite lattice.
for all Q in
Pa
- the point group of the austenite lattice.
From the Polar Decomposition Theorem, the deformation gradient F can be written as RU, where R is a rotation and U is a positive-definite symmetric matrix.
From frame indifference, the free energy depends only upon the symmetric part U of the deformation gradient F. This matrix U is called the Bain strain, lattice distortion or transformation stretch matrix; while,
from material symmetry, there are other deformations which take the austenite lattice into a martensite lattice. These are the variants of the martensite phase.