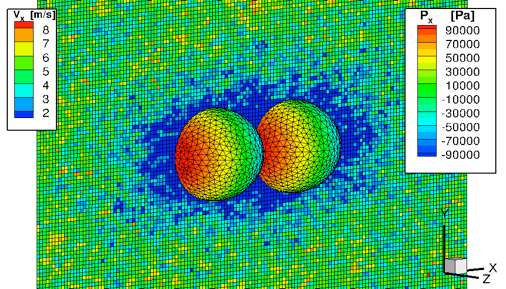
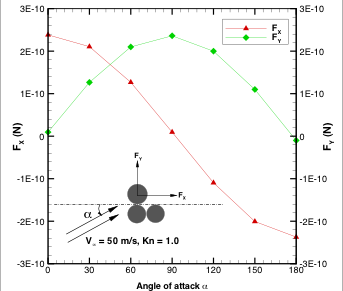
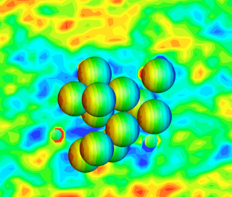
Motivation
In order to characterize nanoparticle pollutants, particles can be given a known charge and accelerated via a known electric field. The measured time of flight is then directly related to the drag force on the particles caused by the surrounding air. If this drag force can be related to nanoparticle cluster geometry and size then such measured time of flight can be used to characterize nanoparticle pollutants in a given sample of plant emissions. Such experimental and theoretical work is the specialty of Prof. Chris Hogan in the Mechanical Engineering department at the University of Minnesota:
http://www.me.umn.edu/people/hogan.shtml
Results and Publications