••1992••
(1)
D. D. Joseph. 1992.
Bernoulli equation and the competition of elastic and inertial pressures in the
potential flow of a second-order fluid,
J.Non-Newtonian Fluid Mech., 42, 385-389.
Abstract
A Bernoullis equation for potential flow of a second order fluid is derived. This equation is used to form an expression for normal extensional stresses at points of stagnation, in which elastic and inertial pressures complete.
Keywords: Bernoullis equation; normal extensional stresses; second order fluid
••1993••
(2)
D. D. Joseph, T. Y. Liao and H. H. Hu. 1993.
Drag and Moment in Viscous Potential Flow,
Eur. J. Mech.
B/Fluids, 12(1), 97-106.
Abstract
We consider solutions of the Navier-Stokes equations in
which the velocity is given by the gradient of a potential. We show that the
drag on bodies and bubbles is the same in viscous and inviscid potential flow.
The lift on two-dimensional bodies is given by the usual Kutta condition but
the moment about the origin of the stresses acting on the body is given by 
where 
is the viscosity, 
is the circulation and 
is the usual moment for an inviscid fluid.
••1994••
(3)
D. D. Joseph and T. Y. Liao. 1994.
Viscous and Viscoelastic Potential Flow,
Trends and
Perspectives in Applied Mathematics, Applied Mathematical Sciences, Sirovich, Arnol'd, eds, Springer-Verlag. Also in
Army HPCRC preprint 93-010., 100, 1-54.
Abstract
Potential
flows of incompressible fluids admit a pressure (Bernoulli) equation when the
divergence of the stress is a gradient as in inviscid
fluids, viscous fluids, linear viscoelastic fluids and second-order fluids. We
show that the equation balancing drag and acceleration is the same for all
these fluids independent of the viscosity or any viscoelastic parameter and
that the drag is zero in steady flow. The unsteady drag on bubbles in a viscous
(and possibly in a viscoelastic) fluid may be approximated by evaluating the
dissipation integral of the approximating potential flow because the neglected
dissipation in the vorticity layer at the
traction-free boundary of the bubble gets smaller as the Reynolds number is
increased. Using the potential flow approximation, the drag 
on
a spherical gas bubble of radius 
rising
with velocity 
in a linear
viscoelastic liquid of density 
and shear modules 
is given by
and in a
second-order fluid by
where 
is the coefficient of
the first normal stress and 
is the viscosity of the fluid. Because 
is negative, we see from this formula that
the unsteady normal stresses oppose inertia; that is, oppose the acceleration
reaction. When is slowly varying, the
two formulas coincide. For steady flow, we obtain 
for both viscous and
viscoelastic fluids. In the case where the dynamic contribution of the interior
flow of the bubble cannot be ignored as in the case of liquid bubbles, the
dissipation method gives an estimation of the rate of total kinetic energy of
the flows instead of the drag. When the dynamic effect of the interior flow is
negligible but the density is important, this formula for the rate of total
kinetic energy leads to 
where 
is
the density of the fluid (or air) inside the bubble and 
is the volume of the
bubble.
Classical
theorems of vorticity for potential flow of ideal
fluids hold equally for viscous and viscoelastic fluids. The drag and lift on
two-dimensional bodies of arbitrary cross section in viscoelastic potential
flow are the same as in potential flow of an inviscid
fluid but the moment 
in
a linear viscoelastic fluid is given by
where 
is
the inviscid moment and 
is the circulation,
and
in a second-order
fluid. When is slowly varying, the
two formulas for coincide.
For steady flow, they reduce to
which is also the
expression for in
both steady and unsteady potential flow of a viscous fluid.
Potential
flows of models of a viscoelastic fluid like Maxwell's are studied. These
models do not admit potential flows unless the curl of the divergence of the
extra-stress vanishes. This leads to an over-determined system of equations for
the components of the stress. Special potential flow solutions like uniform
flow and simple extension satisfy these extra conditions automatically but
other special solutions like the potential vortex can satisfy the equations for
some models and not for others.
(4)
D. D. Joseph and T. Y. Liao. 1994.
Potential Flow of Viscous and Viscoelastic Fluids,
J. Fluid Mech.,
265,
1-23.
Abstract
Potential flows of
incompressible fluids admit a pressure (Bernoulli) equation when the divergence
of the stress is a gradient as in inviscid fluids,
viscous fluids, linear viscoelastic fluids and
second-order fluids. We show that in potential flow without boundary layers the
equation balancing drag and acceleration is the same for all these fluids,
independent of the viscosity or any viscoelastic
parameter, and that the drag is zero when the flow is steady. But, if the
potential flow is viewed as an approximation to the actual flow field, the
unsteady drag on bubbles in a viscous (and possibly in a viscoelastic)
fluid may be approximated by evaluating the dissipation integral of the
approximating potential flow because the neglected dissipation in the vorticity layer at the traction-free boundary of the bubble
gets smaller as the Reynolds number is increased. Using the potential flow approximation,
the actual drag 
on a spherical gas
bubble of radius 
rising with velocity 
in a linear viscoelastic liquid of density 
and shear modules 
is estimated to be
,
and, in a second-order fluid,
,
where 
is the coefficient of
the first normal stress and 
is the viscosity of
the fluid. Because 
is negative, we see
from this formula that the unsteady normal stresses oppose inertia; that is,
oppose the acceleration reaction. When is slowly varying, the
two formulae coincide. For steady flow, we obtain the approximate drag 
for both viscous and viscoelastic fluids. In the case where the dynamic contribution
of the interior flow of the bubble cannot be ignored as in the case of liquid
bubbles, the dissipation method gives an estimation of the rate of total
kinetic energy of the flows instead of the drag. When the dynamic effect of the
interior flow is negligible but the density is important, this formula for the
rate of total kinetic energy leads to 
where 
is the density of the
fluid (or air) inside the bubble and 
is the volume of the
bubble.
Classical theorems of vorticity for potential flow of ideal fluids hold equally
for second-order fluid. The drag and lift on two-dimensional bodies of
arbitrary cross-section in a potential flow of second-order and linear viscoelastic fluids are the same as in potential flow of an
inviscid fluid but the moment 
in a linear viscoelastic fluid is given by
,
where 
is the inviscid moment and 
is the circulation,
and
,
in a second-order fluid. When
is slowly varying, the
two formulae for coincide. For steady
flow, they reduce to
,
which is also the expression
for in both steady and
unsteady potential flow of a viscous fluid. Moreover, when there is no stream,
this moment reduces to the actual moment 
on a rotating rod.
Potential flows of models of
a viscoelastic fluid like Maxwell's are studied.
These models do not admit potential flows unless the curl of the divergence of
the extra stress vanishes. This leads to an over-determined system of equations
for the components of the stress. Special potential flow solutions like uniform
flow and simple extension satisfy these extra conditions automatically but
other special solutions like the potential vortex can satisfy the equations for
some models and not for others.
••1999••
(5)
D. D. Joseph, J. Belanger and G. S. Beavers. 1999.
Breakup of a liquid drop suddenly exposed to a high-speed airstream,
Int. J. Multiphase Flow, 25, 1263-1303.
Abstract
The breakup of viscous and viscoelastic drops in the
high speed airstream behind a shock wave in a shock tube was photographed with
a rotating drum camera giving one photograph every 
. From these photographs we created movies of the fragmentation
history of viscous drops of widely varying viscosity, and viscoelastic drops,
at very high Weber and Reynolds numbers. Drops of the order of one millimeter
are reduced to droplet clouds and possibly to vapor in times less than 
. The movies may be viewed at
http://www.aem.umn.edu/research/Aerodynamic_Breakup. They reveal sequences of
breakup events which were previously unavailable for study. Bag and
bag-and-stamen breakup can be seen at very high Weber numbers, in the regime of
breakup previously called 'catastrophic'. The movies allow us to generate
precise displacement-time graphs from which accurate values of acceleration (of
orders 104 to 105 times the acceleration of gravity) are
computed. These large accelerations from gas to liquid put the flattened drops
at high risk to Rayleigh-Taylor instabilities. The most unstable
Rayleigh-Taylor wave fits nearly perfectly with waves measured on enhanced
images of drops from the movies, but the effects of viscosity cannot be neglected.
Other features of drop breakup under extreme conditions, not treated here, are
available on our Web site.
••2001••
(6)
T. Funada and D. D. Joseph. 2001.
Viscous potential flow analysis of Kelvin-Helmholtz instability in a channel,
J. Fluid
Mech., 445, 263-283.
Abstract
We study the stability of stratified gas-liquid flow in
a horizontal rectangular channel using viscous potential flow. The analysis
leads to an explicit dispersion relation in which the effects of surface
tension and viscosity on the normal stress are not neglected but the effect of
shear stresses are neglected. Formulas for the growth rates, wave speeds and
neutral stability curve are given in general and applied to experiments in
air-water flows. The effects of surface tension are always important and actually
determine the stability limits for the cases in which the volume fraction of
gas is not too small. The stability criterion for viscous potential flow is
expressed by a critical value of the relative velocity. The maximum critical
value is when the viscosity ratio is equal to the density ratio; surprisingly
the neutral curve for this viscous fluid is the same as the neutral curve for
inviscid fluids. The maximum critical value of the velocity of all viscous
fluids is given by inviscid fluids. For air at 20oC and liquids with density 
g/cm3 the liquid viscosity for the critical
conditions is 15 cp; the critical velocity for liquids with viscosities larger
than 15 cp are only slightly smaller but the critical velocity for liquids with
viscosities smaller than 15 cp, like water, can be much lower. The viscosity of
the liquid has a strong affect on the growth rate. The viscous potential flow
theory fits the experimental data for air and water well when the gas fraction
is greater than about 70%.
(7)
T. W. Pan, D. D. Joseph and R. Glowinski. 2001.
Modelling Rayleigh-Taylor instability of a sedimenting suspension of several thousand circular particles in a direct numerical simulation,
J. Fluid Mech., 434, 23-37.
Abstract
In this paper we study the sedimentation of several thousand circular particles in two dimensions using the method of distributed Lagrange multipliers for solid-liquid flow. The simulation gives rise to fingering which resembles Rayleigh-Taylor instabilities. The waves have a well-defined wavelength and growth rate which can be modeled as a conventional Rayleigh-Taylor instability of heavy fluid above light. The heavy fluid is modelled as a composite solid-liquid fluid with an effective composite density and viscosity. Surface tension cannot enter this problem and the characteristic shortwave instability is regularized by the viscosity of the solid-liquid dispersion. The dynamics of the Rayleigh{Taylor instability are studied using viscous potential flow, generalizing work of Joseph, Belanger & Beavers (1999) to a rectangular domain bounded by solid walls; an exact solution is obtained.
••2002••
(8)
D. D. Joseph, G. S. Beavers and T. Funada. 2002.
Rayleigh-Taylor instability of viscoelastic drops at high Weber numbers,
J. Fluid Mech., 453, 109-132.
Abstract
Movies of the breakup of viscous and viscoelastic
drops in the high speed airstream behind a shock wave in a shock tube have been
reported by Joseph, Belanger and Beavers (1999). They performed a Rayleigh-Taylor stability
analysis for the initial breakup of a drop of Newtonian liquid and found that the most unstable Rayleigh-Taylor wave fits nearly perfectly with waves measured on enhanced images of drops from the movies, but the effects of viscosity cannot be neglected. Here we construct a Rayleigh-Taylor stability analysis for an Oldroyd B fluid using measured data
for acceleration, density, viscosity and relaxation time 
. The most unstable wave is a sensitive function
of the retardation time 
which fits
experiments when 
. The growth rates for the most unstable wave are
much larger than for the comparable viscous drop, which agrees with the
surprising fact that the breakup times for viscoelastic drops are shorter. We
construct an approximate analysis of Rayleigh-Taylor instability based on
viscoelastic potential flow which gives rise to nearly the same dispersion
relation as the unapproximated analysis.
(9)
T. Funada and D. D. Joseph. 2002.
Viscous potential flow analysis of capillary instability,
Int. J. Multiphase Flow,
28(9), 1459-1478.
Abstract
Capillary instability of a
viscous fluid cylinder of diameter 
surrounded by another
fluid is determined by a Reynolds number 
, a viscosity ratio 
and a density ratio 
. Here 
is the capillary
collapse velocity based on the more viscous liquid which may be inside or
outside the fluid cylinder. Results of linearized analysis based on potential
flow of a viscous and inviscid fluid are compared with the unapproximated
normal mode analysis of the linearized Navier-Stokes equations. The growth
rates for the inviscid fluid are largest, the growth rates of the fully viscous
problem are smallest and those of viscous potential flow are between. We find that
the results from all three theories converge when 
is large with
reasonable agreement between viscous potential and fully viscous flow with 
. The convergence results apply to two liquids as well as to
liquid and gas.
••2003••
(10)
D. D. Joseph. 2003.
Viscous potential flow,
J. Fluid
Mech., 479, 191-197.
Abstract
Potential
flows 
are solutions of the Navier-Stokes equations for viscous incompressible fluids
for which the vorticity is identically zero. The
viscous term 
vanishes, but the
viscous contribution to the stress in an incompressible fluid (Stokes 1850)
does not vanish in general. Here, we show how the viscosity of a viscous fluid
in potential flow away from the boundary layers enters Prandtl's
boundary layer equations. Potential flow equations for viscous compressible fluids
are derived for sound waves which perturb the Navier-Stokes
equations linearized on a state of rest. These linearized equations support a potential flow with the
novel features that the Bernoulli equation and the potential as well as the
stress depend on the viscosity. The effect of viscosity is to produce decay in
time of spatially periodic waves or decay and growth in space of time-periodic
waves.
In
all cases in which potential flows satisfy the Navier-Stokes
equations, which includes all potential flows of incompressible fluids as well
as potential flows in the acoustic approximation derived here, it is neither
necessary nor useful to put the viscosity to zero.
(11)
D. D. Joseph. 2003.
Rise velocity of spherical cap bubble,
J. Fluid
Mech., 488, 213-233.
Abstract
The
theory of viscous potential flow is applied to the problem of finding the rise
velocity
of a spherical cap bubble
(see Davies & Taylor 1950; Batchelor 1967). The rise velocity is given by
,
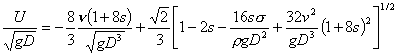where
is the radius of the cap, 
and 
are the density and kinematic viscosity of the liquid, 
is surface tension, 
and 
is the deviation of the
free surface from perfect sphericity 
near the stagnation point 
. The bubble nose is more pointed when 
and blunted when 
. A more pointed bubble increases the rise velocity; the blunter bubble
rises slower. The Davies & Taylor (1950) result arises when 
and vanish; if alone is zero,
,
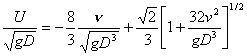showing
that viscosity slows the rise velocity. This equation gives rise to a
hyperbolic drag law
,
which agrees with data on the rise velocity of spherical cap bubbles given by Bhaga & Weber (1981).
(12)
J. Wang and D. D. Joseph. 2003.
Potential flow of a second order fluid over a sphere or an ellipse,
J. Fluid
Mech., 511, 201-215.
Abstract
We study the potential flow of a second-order fluid over a sphere or an ellipse. The normal stress at the surface of the body is calculated and has contributions from the inertia, viscous and viscoelastic effects. We investigate the effects of Reynolds number and body size on the normal stress; for the ellipse, various angles of attack and aspect ratios are also studied. The effect of the viscoelastic terms is opposite to that of inertia; the normal stress at a point of stagnation can change from compression to tension. This causes long bodies to turn into the stream and causes spherical bodies to chain. For a rising gas bubble, the effect of the viscoelastic and viscous terms in the normal stress is to extend the rear end so that it tends to the cusped trailing edge observed in experiments.
(13)
T. Funada and D. D. Joseph. 2003.
Viscoelastic potential flow analysis of capillary instability,
J. Non-Newtonian Fluid Mech., 111, 87-105.
Abstract
Analysis of the linear theory of capillary instability of threads of
Maxwell fluids of diameter D is carried out for the
unapproximated normal mode solution and for a solution based on viscoelastic
potential flow. The analysis here extends the analysis of viscous potential
flow [Int. J. Multiphase Flow 28 (2002) 1459] to viscoelastic fluids
of Maxwell type. The analysis is framed in dimensionless variables with a
velocity scale based on the natural collapse velocity 
(surface tension/liquid viscosity). The collapse
is controlled by two dimensionless parameters, a Reynolds number 
where Oh is
the Ohnesorge number, and a Deborah number 
where 
is the relaxation time. The density ratio 
and 
are nearly zero and do not have a significant
effect on growth rates. The dispersion relation for viscoelastic potential flow
is cubic in the growth rate 
and it can be solved explicitly and computed
without restrictions on the Deborah number. On the other hand, the iterative
procedure used to solve the dispersion relation for fully viscoelastic flow
fails to converge at very high Deborah number. The growth rates in both
theories increase with Deborah number at each fixed Reynolds number, and all
theories collapse to inviscid potential flow (IPF) for any fixed Deborah number
as the Reynolds number tends to infinity.
Keywords: Instability;
Capillary; Viscoelastic; Viscous; Inviscid; Oldroyd
••2004••
(14)
D. D. Joseph and J. Wang. 2004.
The dissipation approximation and viscous potential flow,
J. Fluid
Mech., 505, 365-377.
Abstract
Dissipation approximations have been used to calculate the drag on bubbles and drops and the decay rate of free gravity waves on water. In these approximations, viscous effects are calculated by evaluating the viscous stresses on irrotational flows. The pressure is not involved in the dissipation integral, but it enters into the power of traction integral, which equals the dissipation. A viscous correction of the irrotational pressure is needed to resolve the discrepancy between the zero-shear-stress boundary condition at a free surface and the non-zero irrotational shear stress. Here we show that the power of the pressure correction is equal to the power of the irrotational shear stress. The viscous pressure correction on the interface can be expressed by a harmonic series. The principal mode of this series is matched to the velocity potential and its coefficient is explicitly determined. The other modes do not enter into the expression for the drag on bubbles and drops. They vanish in the case of free gravity waves.
(15)
T. Funada, D. D. Joseph and S. Yamashita. 2004.
Stability of a liquid jet into incompressible gases and liquids,
Int. J.
Multiphase Flow, 30, 1279-1310.
Abstract
We carry out an analysis of the stability of a liquid jet into a gas or another liquid using viscous potential flow. The instability may be driven by Kelvin-Helmholtz KH instability due to a velocity difference and a neckdown due to capillary instability. Viscous potential flow is the potential flow solution of Navier-Stokes equations; the viscosity enters at the interface.
KH instability is induced by a discontinuity of velocity at a gas-liquid interface. Such discontinuities cannot occur in the flow of viscous fluids. However, the effects of viscous extensional stresses can be obtained from a mathematically consistent analysis of the irrotational motion of a viscous fluid carried out here. An explicit dispersion relation is derived and analyzed for temporal and convective/absolute (C/A) instability. We find that for all values of the relevant parameters, there are wavenumbers for which the liquid jet is temporally unstable. The cut-off wavenumber and wavenumber of maximum growth are most important; the variation of these quantities with the density and viscosity ratios, the Weber number and Reynolds is computed and displayed as graphs and asymptotic formulas. The instabilities of a liquid jet are due to capillary and KH instabilities. We show that KH instability cannot occur in a vacuum but capillary instability can occur in vacuum.We present comprehensive results, based on viscous potential flow, of the effects of the ambient.
Temporally unstable liquid jet flows can be analyzed for spatial instabilities by C/A theory; they are either convectively unstable or absolutely unstable depending on the sign of the temporal growth rate at a singularity of the dispersion relation. The study of such singularities is greatly simplified by the analysis here which leads to an explicit dispersion relation; an algebraic function of a complex frequency and complex wavenumber. Analysis of this function gives rise to an accurate Weber-Reynolds criterion for the border between absolute and convective instabilities. Some problems of the applicability to physics of C/A analysis of stability of spatially uniform and nearly uniform flows are discussed.
Keywords: Viscous potential flow; Kelvin-Helmholtz instability; Capillary instability; Temporal instability; Absolute and conveetive instability
(16)
T. Funada, D. D. Joseph, T. Maehara and S. Yamashita. 2004.
Ellipsoidal model of the rise of a Taylor bubble in a round tube,
Int. J. Multiphase Flow, 31, 473-491.
Abstract
The rise velocity of long gas bubbles (Taylor bubbles) in round tubes is modeled by an ovary ellipsoidal cap bubble rising in an irrotational flow of a viscous liquid. The analysis leads to an expression for the rise velocity which depends on the aspect ratio of the model ellipsoid and the Reynolds and Eotvos numbers. The aspect ratio of the best ellipsoid is selected to give the same rise velocity as the Taylor bubble at given values of the Eotvos and Reynolds numbers. The analysis leads to a prediction of the shape of the ovary ellipsoid which rises with same velocity as the Taylor bubble.
••2005••
(17)
J. Wang, D. D. Joseph and T. Funada. 2005.
Purely irrotational theories of the effects of viscosity and viscoelasticity on capillary instability of a liquid cylinder,
J.Non-Newtonian Fluid Mech., 129, 106-116.
Abstract
Capillary instability of a liquid cylinder can arise when either the interior or exterior fluid is a gas of negligible density and viscosity. The shear stress must vanish at the gas-liquid interface but it does not vanish in irrotational flows. Joseph and Wang (2004) derived an additional viscous correction to the irrotational pressure. They argued that this pressure arises in a boundary layer induced by the unphysical discontinuity of the shear stress. Wang, Joseph and Funada (2005) showed that the dispersion relation for capillary instability in the Newtonian case is almost indistinguishable from the exact solution when the additional pressure contribution is included in the irrotational theory. Here we extend the formulation for the additional pressure to potential flows of viscoelastic fluids in flows governed by linearized equations, and apply this additional pressure to capillary instability of viscoelastic liquid filaments of Jeffreys type. The shear stress at the gas-liquid interface cannot be made to vanish in an irrotational theory, but the explicit effect of this uncompensated shear stress can be removed from the global equation for the evolution of the energy of disturbances. This line of thought allows us to present the additional pressure theory without appeal to boundary layers. The validity of this purely irrotational theory can be judged by comparison with the exact solutions of Navier-Stokes equations. Here we show that our purely irrotational theory is in remarkably good agreement with the exact solution in linear analysis of the capillary instability of a viscoelastic liquid cylinder.
Keywords: Capillary instability, Viscoelastic potential flow, Additional pressure contribution, Dissipation method
(18)
J. Wang, D. D. Joseph and T. Funada. 2005.
Pressure corrections for potential flow analysis of capillary instability of
viscous fluids,
J. Fluid
Mech., 522, 383-394.
Abstract
Funada & Joseph (2002) analyzed capillary instability assuming that the flow is irrotational but the fluids are viscous (viscous potential flow, VPF). They compared their results with the exact normal mode solution of the linearized Navier-Stokes equations (fully viscous flow, FVF) and with the irrotational flow of inviscid fluids (inviscid potential flow, IPF). They showed that the growth rates computed by VPF are close to the exact solution when Reynolds number is larger than O(10) and are always more accurate than those computed using IPF. Recently, Joseph & Wang (2004) presented a method for computing a viscous correction of the irrotational pressure induced by the discrepancy between non-zero irrotational shear stress and the zero shear stress boundary condition at a free surface. The irrotational flow with a corrected pressure is called viscous correction of VPF